まえがき

Det Norske Veritas協会の分類基準 AS (DNV)に基づいて、長さ50mを越えた高速双胴船の三次元強度解析が行われます。全長80.1mの船体では、Ruston 16RK 270ディーゼルエンジン四つを装備されており、いずれも時速5、500kW、四つのKaMeWa 80噴射装置より構成される推進システムが備え付けられます。通常速度は47ノット(海里/時間)だが、全速力で走るとなんと53ノットに達します。 正甲板は89の船室から構成される一方、船尾甲板はバスや高速貨物列車のような巨大交通工具を載せることができます。 第二の甲板には、乗客400名が収納できる基本設備を完備されています。
概要
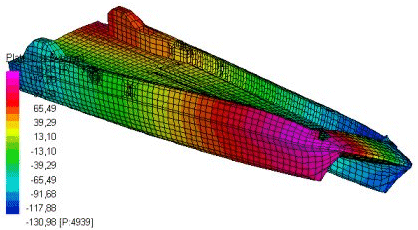
解析では、DNV のHSLC荷重ケースを受ける場合の船体構造挙動を着目しています。下図に示した右舷の有限要素法モデルには、船体の輪郭や一般図から構造設計図細部までほぼ再現され、Strand7のミラー機能によって全体モデルが作成できます。
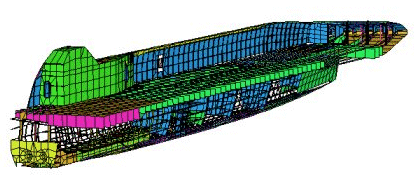
ゴム台に置かれる巨大な船体を解析の対象外だが、これらの反力荷重を考慮されました。
解析では、船体部分は、輪郭、甲板、舷牆、横隔壁、フレームや待合室などを含み、4節点シェル要素で、欄干の手すり、補強材や支柱などは梁要素を用いてモデル化されました。
船体輪郭部分の曲げ、せん断及びねじり効果を解析に全面的に反映されるため、要素のサイズ、種類や数量などを厳選されたうえで、フレーム及び縦方向補強材の間隔に基づいて要素をグレーデイングされました。
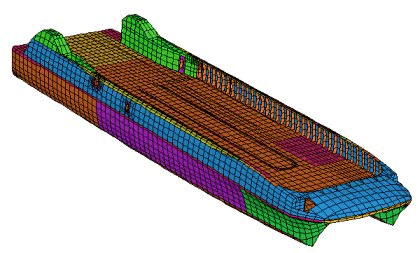
モデルの節点連結線は、船体輪郭と舷牆上の補強材位置が完全に一致し、さらに、慣性修正機能によってこれらの補強材の質量をプレート縁につながった梁要素にまとめました。
メッシュを配置する際、どちら側の補強材の質量も節点連結線にまとめできるように設計されました。なお、補強材要素面積に隣接する要素の面積は慣性修正機能に含まれました。