線形及び非線形時刻歴応答解析

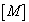質量マトリクス

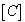減衰マトリクス

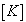剛性マトリクス

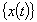節点変位ベクトル

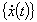節点速度ベクトル

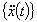節点加速度ベクトル


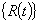荷重ベクトル

1. 動荷重は集中力、集中モーメント、要素荷重、分布荷重または熱荷重のいずれに相当し、荷重係数−時間刻み関係テーブルにより解析モデルに作用します。複数荷重ケースの場合は、一つの荷重条件にまとめ、それぞれの荷重ケースを含まれるか否か荷重係数−時間刻み関係テーブルの荷重係数によります。
   
   
2. 直接積分法を用いられる場合には、荷重と同じ方法で複数の自由度ケースが設定できます。 なお、変位は時間の関数の場合も適応します。
   
   
3. モデル（例えば、固定された節点のあるモデル)の地盤加速度は外力として指定できます。ここで、、時刻歴は任意または荷重係数−時間刻み関係テーブルにより指定され、外力は方向ベクトルによって任意方向で加えます。
   
   

1. 線形静的解を初期条件とする場合、静荷重を受ける構造の変位を指定します。
   
   
2. 過渡解析の解を初期条件とする場合、ある時点の構造動的応答を指定します。この解は選択された任意ステップからのものとします。
   
   
3. 構造任意自由節点の初期速度および加速度。

モード重合法
この方法は、おのおのの振動モードを別々求めてから構造全体の応答を合成する方法で、線形時刻歴解析のみ適用します。

また、時刻歴解析の場合、レーリー減衰以外（また、かわりに)モーダル減衰が利用でき、実験データが得られる場合、減衰の精度がよくなります。

モード重合法は、低次振動数を応答（例えば、地震応答)に占める割合の高い構造に最適であり、殆ど１０次までのモードだけでよい精度が得られます。衝撃荷重に関する問題の場合、５０次またはそれ以上の高次モードが必要となるため、計算時間が長くかかるだけではなく、膨大なデータを記憶し切れないかもしれません。なお、この方法の重大な欠点は、非線形問題に対応しません。

全体系法（直接積分法)

この方法には、モード数に関する制限はないが、 すべての節点変位は運動方程式から直接積分によって求めるため、コストが非常に高いのです。なお、この方法は直接積分法とも呼ばれます。

• 初期条件に基づき、節点変位、速度及び加速度ベクトルを初期化します。
  
  
• モード重ね合せのため、等価要素断面力及び節点外力ベクトルを計算し全体系に加えます。地盤加速度を考慮した場合、等価荷重ベクトルを計算するため、全体質量マトリクスを作成しておきます。
  
  
• 直接積分法において、要素剛性マトリクス、質量および減衰マトリクス、等価要素断面力と節点外力ベクトルを計算しておきます。 剛性を計算する際、温度依存性のある材料も考えられます。さらに、初期条件を設定すれば、要素幾何剛性マトリクスやレーリー減衰、要素材料減衰も考慮されます。なお、オプション設定を変えれば、一致または集中等価荷重ベクトルのいずれを計算できます。拘束条件を考慮し強制変位やリンクなどの定数を釣合い方程式に付け加えると、次の運動方程式が得られます。
  

• 直接積分法を用いる場合、全体剛性マトリクスは次のように表れます。
  
  
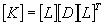
• Ｗｉｌｓｏｎ−θ法あるいはＮｅｗｍａｒｋ−β法のいずれを利用し、指定した時間ステップまで繰返し、変位、速度および加速度を算定します。地盤加速度を用いる場合、変位、速度および加速度の相対値または絶対値が計算されます。
• 要素の応力とひずみを計算します。
  

• 指定した初期条件に従い、節点変位、速度及び加速度ベクトルを初期化します。再計算の場合、現時点において要素変位または応力状態に関するすべての変数は初期条件及び一時結果ファイルの両方を回復されます。
  
• 現在時間ステップは直前のステップと異なる場合は、新しい時間ステップをスタートし、時間積分に必要な常数を算出します。
  
• 要素剛性マトリクス、等価要素断面力ベクトルおよび節点外力ベクトルを計算し釣合い方程式を組み立てます。剛性を計算する際、材料の温度依存性が考えられます。さらに、材料／幾何非線形を考慮することによって、現時点での材料弾性係数及び幾何形状が用いられます。オプションを設定しておくと、要素の幾何剛性マトリクスも一致または集中等価荷重ベクトルのいずれを計算できます。最後、拘束条件を考慮し強制変位やリンクなどの定数を釣合い方程式に付け加えます。よって、構造全体の剛性マトリクス、質量マトリクス、減衰マトリクス及び節点外力ベクトルが作成されます。
  
• Newmarkーβ法により節点変位、速度及び加速度ベクトルを計算されてから、現在変位ベクトルを更新されます。
  
• 収束基準
  
  変位ノルマ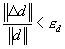
  
  
  
  

  残留力ノルマ
  
  
  
  
  

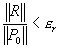
  ここに
  

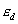  及び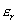は変位と残留力の収束誤差許容値；
  
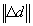  及び 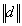は増分と全体変位ベクトルノルマ；
  
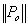  は各時間ステップにおいて最初繰返し計算時の残留力ベクトルノルマ；
  
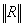  は現時点の残留力ベクトルノルマ。
  
  

  以上の収束基準をすべて満足されば、次の荷重ステップへ進むか最終荷重ステップに中止します。そうでなければ、繰返しが続けます。

注：

1. 時刻歴解析の結果は継続時間内にあたってたくさんの不連続点からリストされます。ソルバーパラメータにより時間刻みを設定しておくと、結果数及び出力間隔が変更できます。 出力可能な解析結果は、指定時刻の節点変位、速度、加速度あるいは要素応力やひずみなどとなります。
   
2. 時間刻みを正しく選択することは、構造応答を見逃さないための重要な一環で、非線形解析にとっては特に不可欠です。そうしないと、結果の安定性及び収束性が保証できません。

一般に、時間刻みが細かくすればするほど、結果が良くなるという。しかし、時間刻みが細かくすると、結果は収束できるまで時間がかかるため、最小時間刻みを制限する必要があります。時間刻みの制限値は結果の計算予測時間より、時間ステップの制限値は設ける結果点数により設定されます。なお、結果点数を物理的に記憶できます。ここで、Strand7には、定期保存オプションにより時間ステップに関する制限を削除されることが要注意。

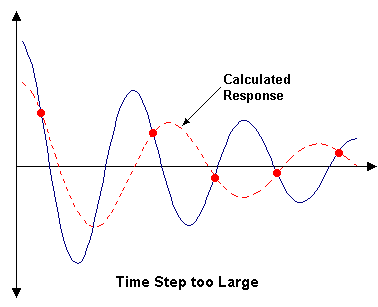
時間刻みは高次振動数よりかなり大きい場合には、構造応答が得られない可能性があります。結果があるとしても、下図に示すように、構造挙動が適切に反映されないかもしれません。