下記の固有値問題よる線形座屈の解が得られます。
ここに
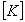全体剛性マトリクス 
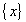座屈モードベクトル
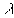座屈荷重係数 
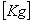全体幾何剛性マトリクス
幾何剛性マトリクスは、初期応力剛性マトリクスとも呼ばれ、要素応力レベルで構成される対称マトリクスで、既知応力状態より定められる要素断面力ベクトルの幾何的な変化を反映されます。例えば、梁とプレートの曲げを考慮する構造の場合は、幾何剛性マトリクスは引張軸／膜応力の補強効果を評価します。
座屈問題は、構造物現時点の応力状態を決められる場合のみ解が得られます。但し、各要素の幾何剛性マトリクスが必要とします。Strand7では、線形や非線形静的解析結果のいずれも線形座屈解析の初期条件として利用できます。
解析手順は下記のとおりです。
- まず、各要素の剛性マトリクス、等価断面力および節点外力ベクトルを計算し組み立てます。剛性を計算する際、ユーザ指定した温度ケースによって材料温度特性を考慮できます。さらに、オプション設定を変えれば、一致または集中等価荷重ベクトルのいずれを計算できます。なお、拘束条件を考慮し方程式を修正します。
初期条件ファイルは非線形静的解析によるものでしたら、計算時点の材料状態及び幾何形状を基に剛性マトリクスが計算されます。即ち、降伏点に達した材料に対して降伏弾性係数を、初期条件に幾何非線形を考慮した場合に対して変形後の幾何形状を用いられます。 幾何剛性マトリクスのため応力を計算する際、初期条件に熱ひずみを含まれるソルバーが利用されます。
- モード周辺のある値を求める際、シフト値が用いられるため、剛性マトリクスを修正されます。
- 座屈荷重係数及び対応する座屈モードを算定する場合、サブ空間反復法（Sub-Space Iteration Method)が使われます。
注：
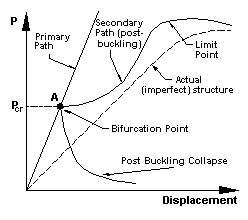
- 線形座屈問題には、初期座屈と後座屈ルートと交差する分岐点（下図のA点)が存在すると仮定します。しかし、この点において平衡状態は一つとは限らず、荷重レベルはこの点を越えたら、後座屈状態に入ります。後座屈特性の決め手は分岐点の二次勾配です。この値は正となる場合、構造は後座屈強度を有して；負となれば構造は座屈しているまたは簡単に崩壊していることを示します。
- 実際の構造物は幾何形状上の欠陥あるいは荷重の不備があるため、初期曲線に従うことが多く分岐点がありません。
- もう一つの仮定は、要素の応力は荷重に比例して変化するという。但し、変形が大きすぎると応力分布を乱れてしまい、線形座屈解析の結果は無効となります。この場合、構造耐力を予測するため非線形解析が望ましい。
- 実際の構造物の初期設計段階において、様々なパラメータの影響を検討するため、線形座屈解析は最適です。
以上の仮定をすべてあるいはほぼ満足すれば、精密解が得られます。より正確な座屈荷重を求める場合、非線形解析を行い、後座屈変形効果のほか、後座屈耐力も予測できます。
- 線形座屈解析の初期条件として、線形静的荷重の組合せも利用できます。